申请日2014.04.12
公开(公告)日2014.07.23
IPC分类号G06N3/08
摘要
基于尖峰自组织径向基神经网络的污泥体积指数SVI的预测方法既属于控制科学与工程领域,又属于环境科学与工程领域。针对污水处理过程中污泥膨胀动力学特性复杂、关键参数难以测量等问题,本发明实现了污泥膨胀的准确预测;该预测方法通过同时调整径向基神经网络的结构和连接权值,提高神经网络的信息处理能力,提升污泥体积指数SVI的预测精度;实验结果表明该智能预测方法能够准确地预测污泥体积指数SVI,促进污水处理过程的高效稳定运行。
摘要附图
权利要求书
1.基于尖峰自组织径向基神经网络的污泥体积指数SVI的预测 方法,其特征在于,包括以下步骤:
(1)确定软测量模型的辅助变量:采集污水处理厂实际水质参数 数据,选取与污泥体积指数SVI相关性强的水质变量溶解氧浓度DO、 酸碱度pH、化学需氧量COD及总氮TN作为污泥体积指数SVI测量 的辅助变量;
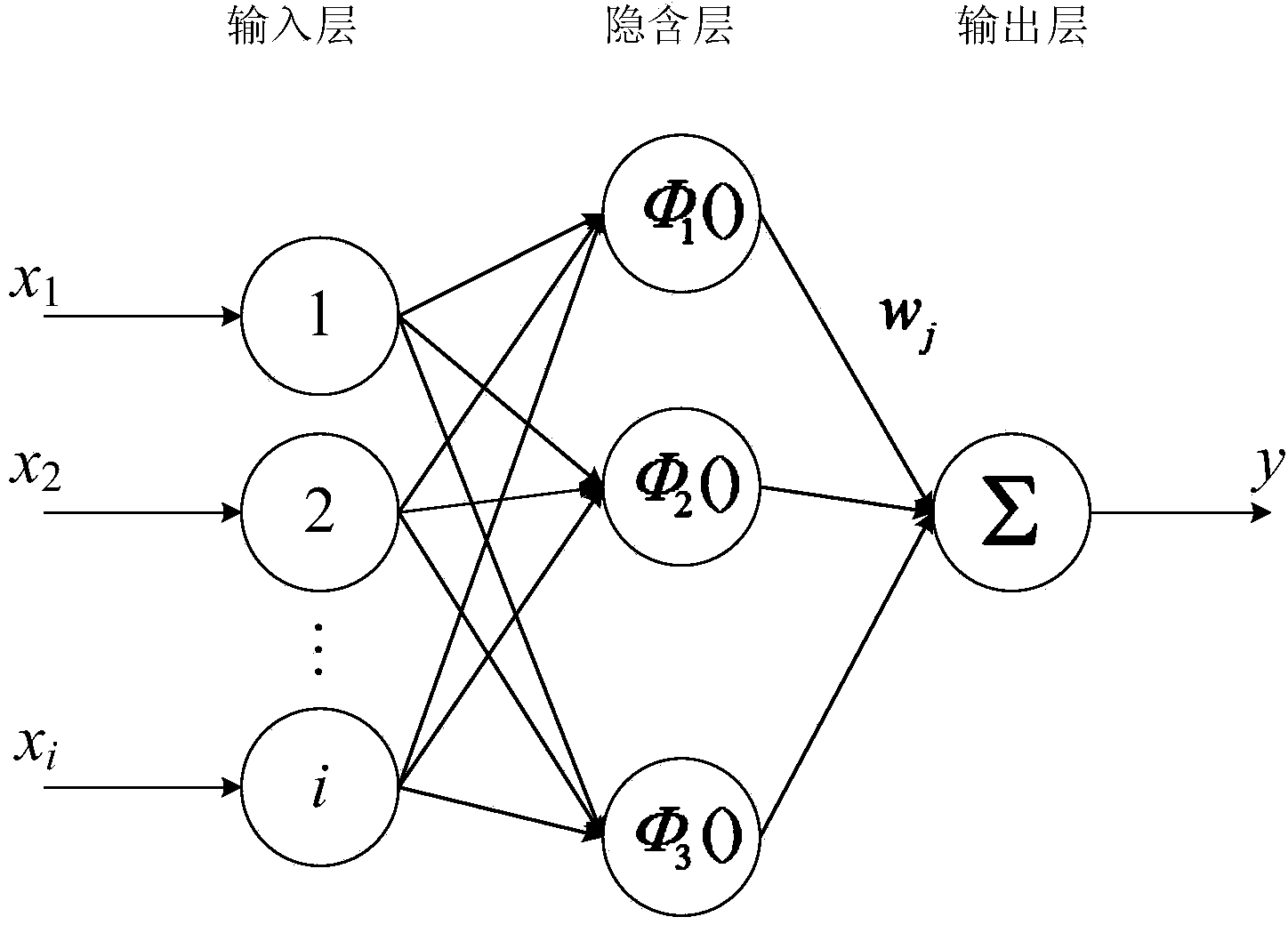
(2)设计用于污泥体积指数SVI的尖峰自组织径向基神经网络拓 扑结构,尖峰自组织径向基神经网络分为三层:输入层、隐含层、输 出层;初始化尖峰自组织径向基神经网络:确定神经网络4-J-1的连 接方式,即输入层神经元为4个,隐含层神经元为J个,输出层神经 元为1个;设共有T个训练样本,第t个训练样本为x(t)=[x1(t),x2(t), x3(t),x4(t)],输出为污水处理系统污泥体积指数SVI预测值y(t),o(t) 表示为神经网络的期望输出;尖峰自组织径向基神经网络的计算功能 是:
wj(t)表示隐含层第j个神经元和输出层的连接权值,j=1,2,…,J;Φ j是隐含层第j个神经元的输出,其计算公式为:
cj表示隐含层第j个神经元中心值,σj表示隐含层第j个神经元的中心宽 度;
定义误差函数为:
T表示输入尖峰自组织径向基神经网络的训练样本数;
(3)设计用于调整尖峰自组织径向基神经网络模型结构的尖峰函 数,尖峰自组织径向基隐含层神经元的尖峰强度定义为:
ssj表示径向基神经网络的隐含层第j个神经元尖峰强度,Λ∈(0,10], kτ∈[0,2],k∈[0,1];以下数值在所设定范围内的选取以及初值的设 定基本并不影响效果;
(4)训练神经网络,具体为:
①给定一个RBF神经网络,隐含层神经元为J,J取3,输入训练 样本数据x(t),设定隐含层第j个神经元中心值的初值cj;设定隐含层 第j个神经元的中心宽度σj;以及隐含层第j个神经元和输出层的连接 权值wj;w1=0.33,w2=0.31,w3=0.06;c1=[-1.19,-0.20,1.93,-1.89], c2=[-0.32,2.45,1.96,-0.59],c3=[1.38,2.20,-1.10,-1.79];中心 宽度σ1=σ2=σ3=0.50;这段建议只保留在说明书中以扩大保护范围;
②设计计算步骤l=1,设定计算最大循环步骤L,最大循环步骤L 至少大于1000;
③计算隐含层神经元的尖峰强度ssj,如式(4);计算尖峰强度ssj的斜率:
计算神经网络输出的绝对百分比误差:
其中,o(t)表示神经网络的期望输出,y(t)表示神经网络的实际输出;
若同时满足:尖峰强度ssj大于尖峰强度阈值ss0∈[-0.5,0.5]中任意 一个值,以下涉及到大于或小于某个范围均指的是在范围内任意设定 的一个值、尖峰强度函数对隐含层输出的导数为正数、绝对百分比误 差大于0.01,分裂隐含层神经元j,调整神经网络结构,设定新神经元 j-m的初始参数:
其中,α∈[0.95,1.05]和β∈[0,0.1],cj和σj分别是神经元j的中心和中 心宽度,新神经元j-m与输出神经元间的连接权值设定为:
wj-m表示新增神经元与输出神经元之间的连接权值,γm表示新增神经 元的分配参数,wj为分裂前第j个隐含层神经元与输出层神经元的连接 权值,Φj-m为新增神经元的输出值,Φj为分裂前第j个隐含层神经元的 输出,Nnew表示神经网络结构调整时新增加神经元的个数;
④判断新神经元j-m与已存在神经元是否冗余,计算分裂前第j个 隐含层神经元参数向量Vj和新增加隐含层神经元j-m的参数向量Vj-m:
Vj(t)=[cj(t),σj(t),wj(t)],j=1,…,J;
(9)
Vj-m(t)=[cj-m(t),σj-m(t),wj-m(t)]; (10)
其中,J表示隐含层神经元总个数;
若新增神经元参数向量Vj-m与Vj不相等且不线性相关,则增加神 经元j-m并按式(7)-(8)对其参数设定,并更新隐含层神经元数为 J1=J+Nnew-1;否则,不调整神经网络的结构,J1=J;
⑤计算隐含层神经元的不活跃率,
其中,irj为隐含层神经元j的不活跃率,fq是隐含层神经元j的尖峰强度 ssj小于静息尖峰值ssr∈[-2,-5]的次数,fd是神经网络结构调整总次 数;设计神经元不活跃度阈值ir0∈[0.25,1],若
irj>ir0; (12)
删除神经元j,同时,找出剩余神经元中与神经元j欧式距离最近的神 经元j’,并对神经元j’参数进行重新设定为:
其中,c’j’和cj’分别表示删减后和删减前神经元j’的中心设定,σ’j’和σj’分别为神经元j’删减后和删减前的中心宽度设定,w’j’和wj’分别表示删 减后与删减前神经元j’与输出层神经元之间的连接权值,并更新隐含 层神经元数为J2=J1-1;
⑥调整神经网的隐含层与输出层之间的连接权值wj:
(15)
其中,w’j和wj分别表示调整后与调整前神经元j与输出层神经元之间 的连接权值,ηw∈(0,0.002]表示神经网络连接权值学习率;
调整神经网络隐含层径向基函数参数中心宽度σj:
其中,σ’j和σj分别表示调整后与调整前神经元j与输出层神经元之间的 中心宽度,ησ∈(0,0.002]表示神经网络中心宽度学习率;
调整神经网络隐含层径向基函数参数中心值cj
其中,c’j和cj分别表示调整后与调整前神经元j与输出层神经元之间的 中心,ηc∈(0,0.002]表示神经网络中心值学习率;
⑦重复步骤③-⑥,l达到计算设定步骤L时转入步骤⑧;
⑧输入训练样本数据x(t+1),重复步骤②-⑦,所有训练样本训练 结束后停止计算;
(5)将测试样本数据作为训练后的神经网络的输入,神经网络的 输出即为污泥体积指数SVI的预测值,实现污泥膨胀的检测。
说明书
基于尖峰自组织径向基神经网络的污泥膨胀预测方法
技术领域
本发明利用基于尖峰自组织径向基神经网络对污泥膨胀关键指标污泥体 积指数SVI进行预测,实现了污泥膨胀的实时检测。污泥体积指数SVI的实 时预测是实现污泥膨胀控制的重要环节,是污水处理过程正常运行的重要基 础,既属于控制科学与工程领域,又属于环境科学与工程领域。
背景技术
随着国民经济的增长和公众环保意识的增强,污水处理自动化技术迎来 了前所未有的发展机遇。国家水污染防治法中提出提高水的重复利用率,鼓 励科学技术研究和先进适用技术的推广应用。随着我国污水处理设施的大量 建成,设施运营状态受到越来越高的重视。因此,本发明的研究成果具有广 阔的应用前景。
污泥体积指数SVI能够较好的反映污水处理过程活性污泥的凝聚、沉降 性能,是我国目前使用最多的评价污泥性能的参数指标。污泥体积指数SVI 值过低,说明泥粒小,无机物含量高,缺乏活性;污泥体积指数SVI值过高, 说明污泥沉降性能不好,可能已经产生污泥膨胀。一般认为污泥体积指数SVI 值大于150mL/g时发生污泥膨胀。污泥膨胀一旦发生,污水处理过程中污泥 难以沉降、随出水流失,一方面导致出水水质不达标,另一方面导致返回到 曝气池中的污泥量减少,影响污水处理过程正常的运行。污泥膨胀严重时可 导致整个污水处理工艺崩溃,带来巨大的经济和环境损失。因此,实现污泥 体积指数SVI值的快速预测,保证污水处理厂的正常运行,降低污泥膨胀发 生率是污水处理安全运行的基础。
传统污泥体积指数SVI的测量,一般取生物反应器出口处的混合液静止 30分钟,沉淀烘干,得到每克干污泥形成的沉淀污泥体积,进而计算污泥体 积指数SVI。然而,传统方法测量误差较大,历时长,操作繁琐。同时,由于 污泥膨胀发生过程机理特性和动力学特性复杂,各成因因素呈现高度非线性、 强耦合性等特点,很难建立污泥膨胀的机理模型。近年来,随着软测量技术 的发展,软测量方法能够实现一定精度范围内的非线性系统预测,为污泥体 积指数SVI的预测提供了理论基础。近年来,人工神经网络作为一种智能方 法在软测量中得到广泛应用,通过优化神经网络性能,可以提高软测量的精 度,实现污泥体积指数SVI的高精度预测,为污泥膨胀的实时检测提供一种 可行方法。
本发明设计了一种基于尖峰自组织径向基神经网络的污泥体积指数SVI 预测方法,通过构建尖峰自组织径向基神经网络软测量模型,实现污泥膨胀 在线预测。
发明内容
本发明获得了一种污泥膨胀关键参数污泥体积指数SVI的智能预测方法, 该方法基于尖峰自组织径向基神经网络,通过同时调整尖峰自组织径向基神 经网络的结构和参数,提高神经网络自适应能力和预测性能,建立了污泥体 积指数SVI的软测量模型,实现了污泥膨胀的在线预测;
本发明采用了如下的技术方案及实现步骤:
基于尖峰自组织径向基神经网络的污泥体积指数SVI的预测方法,其特征 在于,包括以下步骤:
(1)确定软测量模型的辅助变量:采集污水处理厂实际水质参数数据,选 取与污泥体积指数SVI相关性强的水质变量溶解氧浓度DO、酸碱度pH、化 学需氧量COD及总氮TN作为污泥体积指数SVI测量的辅助变量;
(2)设计用于污泥体积指数SVI的尖峰自组织径向基神经网络拓扑结构, 尖峰自组织径向基神经网络分为三层:输入层、隐含层、输出层;初始化尖 峰自组织径向基神经网络:确定神经网络4-J-1的连接方式,即输入层神经元 为4个,隐含层神经元为J个,输出层神经元为1个;设共有T个训练样本, 第t个训练样本为x(t)=[x1(t),x2(t),x3(t),x4(t)],输出为污水处理系统污泥体积指 数SVI预测值y(t),o(t)表示为神经网络的期望输出;尖峰自组织径向基神 经网络的计算功能是:
wj(t)表示隐含层第j个神经元和输出层的连接权值,j=1,2,…,J;Φj是隐含 层第j个神经元的输出,其计算公式为:
cj表示隐含层第j个神经元中心值,σj表示隐含层第j个神经元的中心宽度;
定义误差函数为:
T表示输入尖峰自组织径向基神经网络的训练样本数;
(3)设计用于调整尖峰自组织径向基神经网络模型结构的尖峰函数,尖峰 自组织径向基隐含层神经元的尖峰强度定义为:
ssj表示径向基神经网络的隐含层第j个神经元尖峰强度,Λ∈(0,10],kτ∈[0, 2],k∈[0,1];以下数值在所设定范围内的选取以及初值的设定基本并不影响 效果;
(4)训练神经网络,具体为:
①给定一个RBF神经网络,隐含层神经元为J,J取3,输入训练样本数据 x(t),设定隐含层第j个神经元中心值的初值cj;设定隐含层第j个神经元的中心 宽度σj;以及隐含层第j个神经元和输出层的连接权值wj;w1=0.33,w2=0.31, w3=0.06;c1=[-1.19,-0.20,1.93,-1.89],c2=[-0.32,2.45,1.96,-0.59],c3=[1.38, 2.20,-1.10,-1.79];中心宽度σ1=σ2=σ3=0.50;这段建议只保留在说明书中以 扩大保护范围;
②设计计算步骤l=1,设定计算最大循环步骤L,最大循环步骤L至少大于 1000;
③计算隐含层神经元的尖峰强度ssj,如式(4);计算尖峰强度ssj的斜率:
计算神经网络输出的绝对百分比误差:
其中,o(t)表示神经网络的期望输出,y(t)表示神经网络的实际输出;
若同时满足:尖峰强度ssj大于尖峰强度阈值ss0∈[-0.5,0.5]中任意一个值, 以下涉及到大于或小于某个范围均指的是在范围内任意设定的一个值、尖峰 强度函数对隐含层输出的导数为正数、绝对百分比误差大于0.01,分裂隐含层 神经元j,调整神经网络结构,设定新神经元j-m的初始参数:
其中,α∈[0.95,1.05]和β∈[0,0.1],cj和σj分别是神经元j的中心和中心宽度, 新神经元j-m与输出神经元间的连接权值设定为:
wj-m表示新增神经元与输出神经元之间的连接权值,γm表示新增神经元的分配 参数,wj为分裂前第j个隐含层神经元与输出层神经元的连接权值,Φj-m为新增 神经元的输出值,Φj为分裂前第j个隐含层神经元的输出,Nnew表示神经网络 结构调整时新增加神经元的个数;
④判断新神经元j-m与已存在神经元是否冗余,计算分裂前第j个隐含层神 经元参数向量Vj和新增加隐含层神经元j-m的参数向量Vj-m:
Vj(t)=[cj(t),σj(t),wj(t)],j=1,…,J; (9)
Vj-m(t)=[cj-m(t),σj-m(t),wj-m(t)]; (10)
其中,J表示隐含层神经元总个数;
若新增神经元参数向量Vj-m与Vj不相等且不线性相关,则增加神经元j-m 并按式(7)-(8)对其参数设定,并更新隐含层神经元数为J1=J+Nnew-1;否则,不 调整神经网络的结构,J1=J;
⑤计算隐含层神经元的不活跃率,
其中,irj为隐含层神经元j的不活跃率,fq是隐含层神经元j的尖峰强度ssj小于 静息尖峰值ssr∈[-2,-5]的次数,fd是神经网络结构调整总次数;设计神经元不 活跃度阈值ir0∈[0.25,1],若
irj>ir0; (12)
删除神经元j,同时,找出剩余神经元中与神经元j欧式距离最近的神经元j’, 并对神经元j’参数进行重新设定为:
其中,c’j’和cj’分别表示删减后和删减前神经元j’的中心设定,σ’j’和σj’分别为 神经元j’删减后和删减前的中心宽度设定,w’j’和wj’分别表示删减后与删减前 神经元j’与输出层神经元之间的连接权值,并更新隐含层神经元数为J2=J1-1;
⑥调整神经网的隐含层与输出层之间的连接权值wj:
其中,w’j和wj分别表示调整后与调整前神经元j与输出层神经元之间的连接权 值,ηw∈(0,0.002]表示神经网络连接权值学习率;
调整神经网络隐含层径向基函数参数中心宽度σj:
其中,σ’j和σj分别表示调整后与调整前神经元j与输出层神经元之间的中心宽 度,ησ∈(0,0.002]表示神经网络中心宽度学习率;
调整神经网络隐含层径向基函数参数中心值cj
其中,c’j和cj分别表示调整后与调整前神经元j与输出层神经元之间的中心,ηc∈(0,0.002]表示神经网络中心值学习率;
⑦重复步骤③-⑥,l达到计算设定步骤L时转入步骤⑧;
⑧输入训练样本数据x(t+1),重复步骤②-⑦,所有训练样本训练结束后停 止计算;
(5)将测试样本数据作为训练后的神经网络的输入,神经网络的输出即为 污泥体积指数SVI的预测值,实现污泥膨胀的检测。
本发明的创造性主要体现在:
(1)本发明针对当前活性污泥法污水处理过程污泥膨胀难以检测的问题, 通过确定污泥体积指数SVI的辅助变量,采用自组织径向基神经网络建立污泥 体积指数的软测量模型,实现污泥体积指数SVI的预测,完成污泥膨胀的检测;
(2)本发明设计了基于生物尖峰神经元工作方式的尖峰强度增长修剪机 制,实现了径向基神经网络的自组织设计,提高了径向基神经网络的性能, 改善了污泥体积指数SVI的预测精度,对于时变系统能够较好的在线预测;
特别要注意:本发明只是为了描述方便,采用的是对污泥体积指数SVI 值的预测,同样该发明也可适用污水处理其他关键水质参数的预测,只要采 用了本发明的原理进行预测都应该属于本发明的范围。






