城市污水处理过程出水指标在线软测量预测方法

　　申请日2013.10.23

　　公开(公告)日2014.03.12

　　IPC分类号G06F19/00

　　摘要

　　本发明公开了一种城市污水处理过程出水指标在线软测量预测方法，该方法首先采用以相关性为原则和递归偏最小二乘法为局部模型的即时学习模型结构，同时基于统计学习理论对模型自身不确定性进行描述，该模型可以充分反映污水处理过程不确定性、大滞后等特点，预测结果的解释性更强，控制人员可以及时调整曝气池的曝气量、回流量等工艺变量，维持物料平衡和细菌种群平衡，充分实现有机物的高效去除。

　　权利要求书

　　1.一种城市污水处理过程出水指标在线软测量预测方法，其特征在于，包括以下步骤：

　　1)将从污水厂获取的数据中去除超过标准差3倍的数据，之后再将余下数据进行标准化处理：

　　 $x_{i, m} = \frac{x_{i} - m}{s}$

　　其中，xi，m是xi的转换形式，i=1，2，…，N，m和s分别是均值和标准差;

　　2)将处理后的数据作为模型的训练集合，并把训练集合数据放在空间G中;

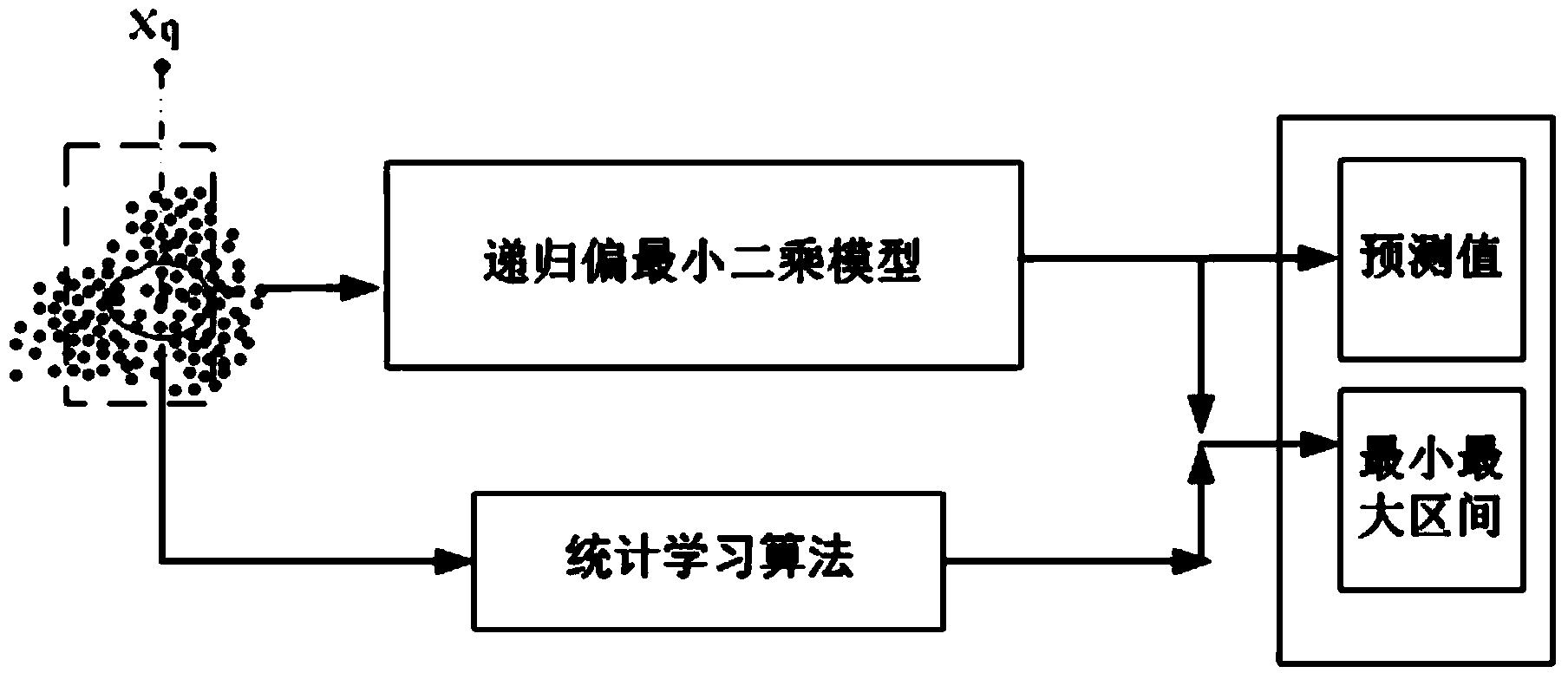
　　3)现场测量获取一个新数据点后，开始建立局部模型：

　　①根据新来数据点选择与之相关的数据

　　首先引入Ci，j对其相关性进行衡量：

　　x′i=xi-xq

　　x′j=xj-xq

　　 $C_{i, j} = \frac{x_{j}^{'} x_{i}^{' T}}{| | x_{i}^{'} | | | | x_{j}^{'} | |} > r$

　　其中，xi和xj是空间集合G中的数据，xq是新数据，随后选择相关系数Ci，j的数据并置于相关数据空间Z中，考察空间Z中的样本数是否大于数据的维数，如果大于则下一步，否则按r=r-δ放松相关限r的限制，使空间Z中的样本数大于数据的维数，按此逻辑，重新计算Ci，j，之后再进一步计算主元分析PCA指标，进而加深数据选择的相关性，如下情况：

　　假设B=[X，Y]是n×m的数据矩阵，PCA将多变量的输入数据矩阵进行奇异值分解后得到主元和特征向量：

　　 $B = {TP}^{T} = t_{1} p_{1}^{T} + t_{2} p_{2}^{T} + . . . + t_{m} p_{m}^{T} + ϵ$

　　其中，ti∈Rn被称为得分向量，即矩阵B的主元，pi∈Rm被称为负荷向量， ε是残差矩阵，它包含了系统的数据的主要噪声，T=[t1，t2，…，tn]和 P=[p1，p2，…，，pm]分别是得分向量矩阵和负荷向量矩阵，当给定一个新的采样向量，PCA的得分向量、预测和残差向量的关系如下：

　　 $t_{i} = {bp}_{i}, \hat{b} = bC, \tilde{b} = b (I - C)$

　　其中，C=PTP，是预测值，是残差，采样向量被映射到了主元空间和残差空间，即，

　　 $b = \hat{b} + \tilde{b}$

　　统计量Q主要用于测量残差数据的变化

　　 $Q = {| | \tilde{b} | |}^{2} = b (I - C) b^{T}$

　　Q统计量是衡量原始数据和主元分析PCA处理后数据的差异性的指标，此外，为了避免模型外推误差，引入了T2统计量指标，T2统计量定义如下：

　　 $T^{2} = Σ_{i = 1}^{l} \frac{t_{l}^{2}}{σ_{t_{l}}^{2}}$

　　其中，表示第l个得分tl的标准差，l的确定是对进行累加计算，直到所对应的l值，T2统计量越小，则表示采样数据靠近模型数据的均值，Q统计量和T2统计量能作为综合指标来衡量数据的差异，J越小说明数据的相关性越强，否则相反，

　　J=λT2+(1-λ)Q

　　其中，T2和Q可由上述统计量计算公式算得，通常λ设置为0.9，

　　确定最终数据选择指标J，并根据相应的J选择相对最相关的数据放于相应的数据库L中用于后续递归偏最小二乘算法的建模;

　　②建立回归偏最小二乘模型

　　根据相关数据集合，即数据库L，计算CPLS和相应的预测值：

　　CPLS=(XTX)+XTY;ynew，=CPLSxq

　　其中，X是数据库L中的与xq相关性最大的输入数据，Y是数据库L中的需要预测的历史值，而0+是右逆，CPLS是PLS算法的回归系数;

　　③对于新来的数据点，除了利用数据库L来训练回归模型外，利用校验集合来计算每个输出值的p值，因此，每次只需计算新的数据点xq的可能分配到yq的值，将作为p值处理：

　　 $p ((x_{1}, y_{1}), \cdot \cdot \cdot, (x_{d}, y_{d}), (x_{q}, y_{q})) = p (y_{q}) = \frac{# {i = n + 1, . . ., d, q : α_{i} &GreaterEqual; α_{q}^{y_{q}}}}{d - n + 2}$

　　其中，#A代表了集合A中元素个数，若可以计算校验集合中每个可能输出的p值，所有输出的p值在置信度δ以内则其至少有δ概率发生故障，因此，给定置信度1-η，ICP算法的输出为：

　　{yq：p(yq)>η}，

　　一致性测量指标是用来衡量真实输出值yi和预测值而可由计算得出，相对于采样点xi的重要指标，定义为真实值和预测值的绝对误差：

　　 $α_{i} = | y_{i} - {\hat{y}}_{i} |$

　　以降序的方式排列计算所得αn+1，…，αd，在此基础上计算有上公式计算 p(yq)，再通过比例公式推断得出其中，σB和σp分别是空间G数据点标准偏差和对应获得输出新数据点的标准偏差，从而可确定其不确定区间为(-2σp，2σp);

　　4)当新数据xq更新后，回到步骤3)计算新数据预测值ynew。

　　2.根据权利要求1所述的一种城市污水处理过程出水指标在线软测量预测方法，其特征在于：步骤3)中第③点所述的校验集合是空间G中与新来数据点时间最近的，新来采样时刻d的采样点以前的一段数据。

　　说明书

　　一种城市污水处理过程出水指标在线软测量预测方法

　　技术领域

　　本发明涉及城市污水处理的技术领域，尤其是指一种基于即时学习算法和统计学习理论提出了带有模型不确定描述的城市污水处理过程出水指标在线软测量预测方法。

　　背景技术

　　污水处理是采取特定工艺将污水中的污染物分离出去或将其转化为无害物质，从而净化污水的一个过程。但是污水处理过程的生产条件恶劣，随机干扰严重，并且具有多输入、多输出、不确定性、强非线性、大滞后、大时变等特点，使得该过程发杂，难以用机理模型进行准确的描述。此外，由于污水处理系统复杂性，有一些重要出水指标(如BOD5、COD、SVI等)无法在线实时测量，BOD5是污水处理过程中重要的出水指标，用于检测水体中有机污染物情况，它直接影响着污水厂的生产运行。研制新型硬件检测仪表虽然可以直接解决 BOD5的检测问题，但是污水处理过程反应复杂，导致硬件仪表的检测精度有限，在线仪表维护成本高。污水处理的生化反应过程易受污水的浓度、天气、气温、时间变化的影响，国际水质协会IWA(International Water Association)制定的污水生化处理过程的标准模型是在特定的环境下制定出来的，具有很大的局限性。当污水的浓度、天气、气温、时间变化时，所反映出的溶解氧和出水指标值与标准模型得出的值有很大的偏差。需要针对污水处理的生化反应特点，根据污水处理厂的实际检测数据，进行出水水质预测模型研究，借助建模的各种理论与方法，包括数据的预处理、模型的建立、模型的校正等环节，为污水处理厂建立适用的出水水质预测模型。软测量为此提供了新的解决途径，其基本思路是通过易于在线测量的变量建立合适的模型预测难于测量的变量。近年来软测量技术获得了长足的发展，其研究领域涉及到石油、化工、环保等领域。

　　现有的污水水质软测量预测模型(例如基于神经网络的预测模型等)都未考虑实际的污水处理过程中，作为模型输入变量的关键工艺参数的检测仪表容易漂移甚至故障的问题，本发明不仅通过软测量模型预测水质关键参数，同时对模型偏差进行在线修正，对模型不确定性进行数学描述，作为模型预测准确性评价。

　　发明内容

　　本发明的目的在于克服现有技术的不足，提供一种城市污水处理过程出水指标在线软测量预测方法，该方法不仅能够提供污水水质出水指标的预测值，同时给出了基于统计学习理论的模型不确定性描述，充分反映污水处理过程不确定性、大滞后等特点，根据软测量预测结果，控制人员可以及时调整曝气池的曝气量、回流量等工艺变量，维持物料平衡和细菌种群平衡，充分实现有机物的高效去除。

　　为实现上述目的，本发明所提供的技术方案为：一种城市污水处理过程出水指标在线软测量预测方法，包括以下步骤：