污水处理过程自适应广义控制方法及系统

发布时间：2018-4-24 11:53:30  中国污水处理工程网

　　申请日2015.03.02

　　公开(公告)日2015.08.26

　　IPC分类号G05B13/04; G05D11/13

　　摘要

　　本发明公开了一种污水处理过程自适应广义预测控制方法，包含以下顺序的步骤：首先利用反馈线性化的思想来实现自适应广义预测控制器的设计;然后在证明其李雅普诺夫稳定的同时，得到修正系统CARIMA模型参数的自适应规则，来动态调整模型参数使得系统跟踪误差达到最小，实现溶解氧浓度的稳态控制。本发明的控制方法及系统，解决了普通广义预测控制在应对较大干扰时不能实现稳定控制的问题。实验结果表明该控制算法能够稳定、快速地控制溶解氧浓度，具有较强的抗干扰能力，有利于实现污水处理过程的稳定、高效运行。

　　摘要附图

 

　　权利要求书

　　1.一种污水处理过程自适应广义预测控制方法，其特征在于，包含以下顺 序的步骤：

　　A、首先利用反馈线性化的思想来实现自适应广义预测控制器的设计;

　　B、然后在证明其李雅普诺夫稳定的同时，得到修正系统CARIMA模型参数 的自适应规则，来动态调整模型参数使得系统跟踪误差达到最小，实现溶解氧 浓度的稳态控制。

　　2.根据权利要求1所述的污水处理过程自适应广义预测控制方法，其特征 在于，具体包含以下顺序的步骤：

　　S1.确定控制系统，即GPC控制器：针对厌氧-缺氧-好氧活性污泥系统中的 溶解氧浓度进行控制，以好氧池中的溶解氧浓度为被控量，以相应池中的氧传 递系数为控制量;

　　S2.模糊神经网络模型：

　　采用TSK模型的形式，输出变量见式(1)所示：

　　$y(x_1,x_2,..,x_4)=\underset{j=1}{\overset{u}{\Sigma }}{w}_j\·{\phi }_j={\Theta }^T\left(k\right)\Psi \left(k\right)---\left(1\right)$

　　其中，u是训练所得到的模糊规则个数，wj是模糊系统的结论权值，φj为模 糊系统的各隶属度函数，令Aj=(α1j,α2j,...,αrj)，α表示wj的参数，X=(x1,x2,…,xr)， 则Ψ(k)=[φ1X,..,φuX]T;

　　S3.反馈线性化思想：

　　考虑如下的一类非线性离散系统动态模型：

　　$\left\{\begin{array}{c}{x}_n(k+1)=f\left[x\left(k\right)\right]+g\left[x\left(k\right)\right]u\left(k\right)\\ y(k+1)=x_n(k+1)\end{array}\right.---\left(2\right)$

　　其中，x(k)=[x1(k),x2(k),..,xn(k)]T=[x(k),x(k-1),..,x(k-n+1)]T是系统状态向量，u是 系统输入，y是系统输出，f[x(k)]和g[x(k)]是未知函数;

　　假定|g[x(k)]|>ε成立，其中ε是一个足够小的正实数，由此可以得知模糊模型 的相对度等于1;

　　针对上述所示的非线性系统(假设Lh[x(k)]g[x(k)]=g[x(k)]≠0)，选择如下的控制 率：

　　$u_{*}=\frac{1}{g\left[x\left(k\right)\right]}[-f[x\left(k\right)]+v\left(k\right)]---\left(3\right)$

　　而对于控制目标是跟踪指定轨迹xnd的情况，且该预定轨迹是有界的，可以 选择v(k)：

　　v(k)=xnd(k+1)-kne(k-n+1)-…-k1e(k)=xnd(k+1)-kTe(k) (4)

　　其中，e(k)=x(k)-xd(k)是跟踪误差，e(k)=[e(k-n+1),...,e(k-1),e(k)]T，ki(i=1..n) 是指定参数，k=[kn,kn-1,..,k1]T，以使得系统输出可以渐进收敛到指定轨迹，此时 可以得到系统闭环误差方程为：

　　e(k+1)=-kTe(k) (5)

　　由此，将式(4)带入式(3)中，并与式(2)相减得到下式(6)，得到系 统输出误差与控制率之间的闭环动态方程：

　　e(k+1)=-kTe(k)+g[u*(k)-u(k)] (6)

　　S4.设计广义预测控制器

　　广义预测控制算法中，采用公式(7)所示的受控自回归积分滑动平均模型 (CARIMA)作为被控系统的数学模型;

　　A(z-1)y(t)=B(z-1)u(t-1)+C(z-1)w(t)/Δ (7)

　　其中，A(z-1)、B(z-1)和C(z-1)是z-1的多项式，z-1表示后移算子，w(t)是系统 干扰;

　　利用Diophantine方程的方法求得广义预测控制律为：

　　u=(GTG+λI)-1GT[yr-Fy(t)-HΔu(t-1)] (8)

　　其中，F、G、H表示所采用Diophantine方程求解控制律的参数向量，λ表 示控制权值，yr表示指定参考轨迹，y(t)表示系统输出，Δu(t-1)表示所求的控制 增量，I表示单位向量;

　　S5.设计T-S模糊模型结论参数的自适应规则

　　由系统输出误差与控制率之间的闭环动态方程的向量形式见式(9)：

　　e(k+1)=Λe(k)+bg[u*(k)-u(k)] (9)

　　其中Λ、bg是闭环动态方程的参数，u*(k)是所选择的期望控制率，e(k)表示 系统误差向量，u(k)表示控制变量;

　　由广义预测控制算法得到的控制增量，得到如下的广义预测控制的控制率， 如式(10)所示：

　　u(k)=K[ΦR-Fy(k)]+u(k-1) (10)

　　K=GT/(GTG+λ)

　　其中，G、F是求解广义预测控制率过程中所用到的参数，R是指定轨迹， λ是控制加权常数，u(k)表示控制变量，y(k)表示被控变量，Φ表示反馈增益向量， 这里取作单位向量;

　　由动态模糊神经网络建模方法得到的系统模型式(1)作为上述控制率 表达式中的系统输出y(k)的估计，从而可以得到该控制率u(k)以及相应的最优控 制率u*(k)为：

　　$\begin{array}{c}u\left(k\right)=u[x_e\left(k\right),\hat{\Theta }]\\ K=[\mathrm{\Phi R}-F\hat{y}\left(k\right)]+u(k+1)\\ =K[\mathrm{\Phi R}-F{\hat{\Theta }}^T\left(k\right)\Psi \left(k\right)]+u(k+1)\end{array}---\left(11\right)$

　　其中，Ψ(k)为模糊神经网络模型系数组合成的参数，Θ*分别表示预测 参数向量、最优参数向量;并以u*作为控制率的最优近似，代入到式(9)中， 得到系统误差与广义预测控制率相关联的系统误差表达式(13)：

　　$\begin{array}{c}e(k+1)=\mathrm{\Lambda e}\left(k\right)+b_g[u^{*}\left(k\right)-u\left(k\right)]\\ =\mathrm{\Lambda e}\left(k\right)+b_g\mathrm{KF}{\hat{\Theta }}^T\left(k\right)\Psi \left(k\right)\end{array}---\left(13\right)$

　　其中，$\tilde{\Theta }\left(k\right)=\hat{\Theta }\left(k\right)-{\Theta }^{*};$

　　考虑如下的李雅普诺夫候选函数V(k)，即可以证明系统在某平衡点的稳定性 的函数，其中r是一个正整数;

　　$V\left(k\right)=\frac{1}{2}{e}^T\left(k\right)\mathrm{Pe}\left(k\right)+\frac{1}{2\gamma }{\tilde{\Theta }}^T(k-1)\tilde{\Theta }(k-1)---\left(14\right)$

　　其中P是所设的一个正定对称矩阵，γ是一个正整数;

　　为了使跟踪误差收敛到0，根据李雅普诺夫稳定性定理，需要使得ΔV(k)<0， 最终得到模型参数的自适应变化率规则如式(15)所示：

　　$\hat{\Theta }\left(k\right)=\hat{\Theta }(k-1)+\gamma {\left[\mathrm{\Lambda e}\left(k\right)\right]}^T{\mathrm{Pb}}_g\mathrm{KF\Psi }\left(k\right)---\left(15\right)$

　　此时，系统跟踪误差收敛下的模型参数自适应证明完毕;

　　S6.应用到BSM1中的溶解氧浓度控制

　　基于TSK模糊模型设计的广义预测控制器，在应用到BSM1中运行过程中， 由式(15)根据系统运行状态动态调整模糊模型结论参数，使其反映系统此时 的动态特性，进而影响到广义预测控制律;通过对A2/O活性污泥处理系统的好 氧池的氧传递系数进行调节，实现溶解氧浓度的稳态控制。

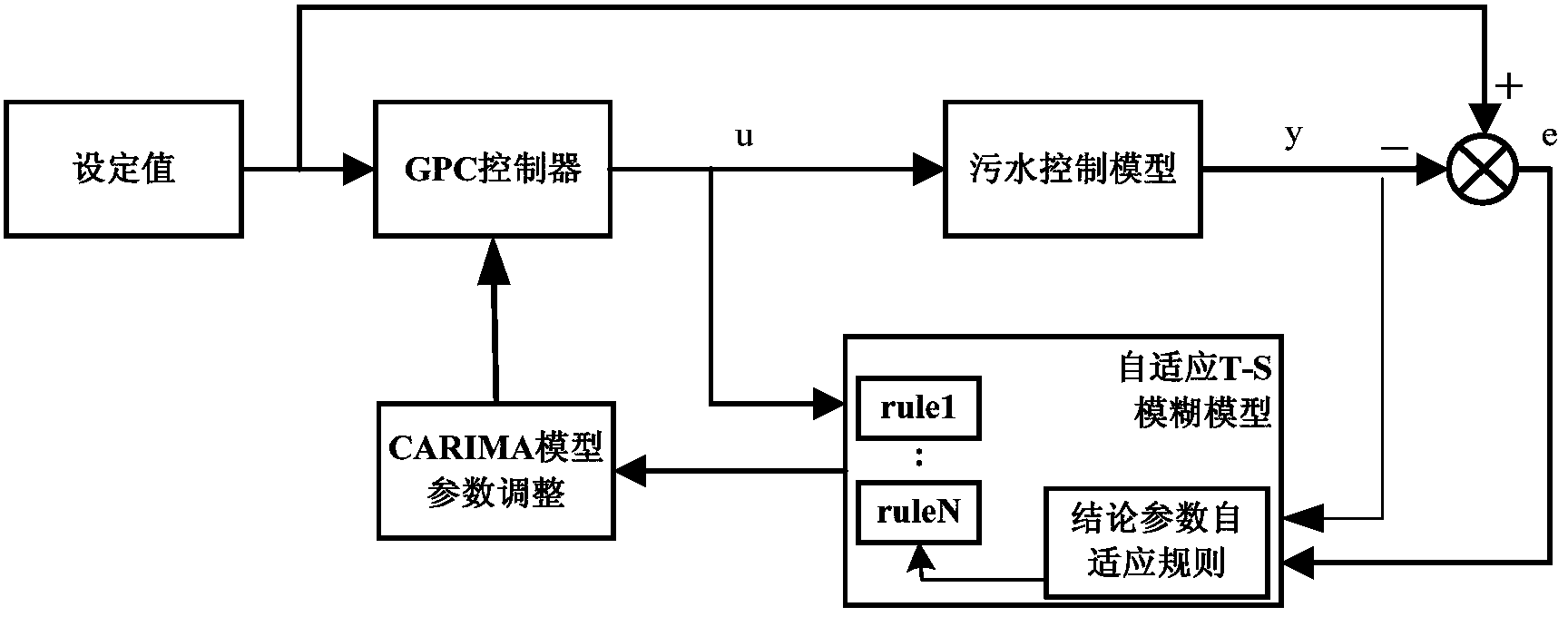
　　3.一种污水处理过程自适应广义预测控制系统，其特征在于：包括顺序相 连的GPC控制器、污水控制模块、反馈线性化模块、广义预测控制器，其中GPC 控制器与广义预测控制器相连。

　　4.根据权利要求3所述的污水处理过程自适应广义预测控制系统，其特征 在于：所述的广义预测控制器是基于TSK模糊模型设计的。

　　说明书

　　一种污水处理过程自适应广义预测控制方法及系统

　　技术领域

　　本发明涉及污水处理领域，特别涉及一种污水处理过程自适应广义预测控 制方法及系统。

　　背景技术

　　当前我国污水处理处于一个前所未有的发展机遇，国家积极推动污泥处理 处置重大技术的研发、示范和推广，开展在线控制技术研究，将污水处理与再 生利用的重大关键技术纳入国家相关科技计划，致力于推进技术先进、经济适 用、环境友好的工艺流程和处理技术。

　　活性污泥污水处理工艺在当前污水处理行业应用广泛，而其中溶解氧浓度 是影响污水处理过程效率、运行费用以及稳定性的主要控制因素。曝气池中氧 气不足和过量都会对微生物生存环境带来不利影响。当氧气不足时，一方面由 于曝气池中丝状菌会大量繁殖，最终产生污泥膨胀;另一方面会降低细菌分解 的效果，延长处理时问，甚至导致生物处理失效。而氧气过量(即过量曝气)则会 由于絮凝剂遭到破坏而导致悬浮固体沉降性变差，同时使能耗过高。因此，溶 解氧浓度先进控制算法具有重要的研究价值。

　　溶解氧浓度控制的难点之一是过程本身的非线性和时变性。当前在实际的 溶解氧控制过程中，开关控制和PID控制是应用最多的控制方法，也有自适应 控制、模糊控制、神经网络控制等方法。前者控制方式简单易于使用，但控制 精度不高、波动大、能耗高;模糊控制则需要掌握大量的现场控制经验知识且 缺乏自学习能力。而且这些控制方法都没有把溶解氧非线性过程模型整合到控 制器的设计当中，不能很准确地反映过程的实际特性。预测控算法将溶解氧浓 度模型应用到控制器的设计中，并取得较好的控制结果，但是当面对较大干扰 情况时，就不能很好的保持溶解氧浓度的稳定。

　　因此，污水处理系统中的溶解氧浓度具有非线性、大时变、大滞后、干扰 严重等特征，设计一种可以跟随污水控制环境变化而做出相应改变的模糊自适 应广义预测控制方法是十分有必要的。

　　发明内容

　　本发明的目的在于克服现有技术的缺点与不足，提供一种污水处理过程自 适应广义预测控制方法。

　　本发明的另一目的在于提供一种污水处理过程自适应广义预测控制系统。

　　本发明的目的通过以下的技术方案实现：

　　一种污水处理过程自适应广义预测控制方法，包含以下顺序的步骤：

　　A、首先利用反馈线性化的思想来实现自适应广义预测控制器的设计;

　　B、然后在证明其李雅普诺夫稳定的同时，得到修正系统CARIMA模型参数 的自适应规则，来动态调整模型参数使得系统跟踪误差达到最小，实现溶解氧 浓度的稳态控制。

　　所述的污水处理过程自适应广义预测控制方法，具体包含以下顺序的步骤：

　　S1.确定控制系统，即GPC控制器：针对厌氧-缺氧-好氧活性污泥系统中的 溶解氧浓度进行控制，以好氧池中的溶解氧浓度为被控量，以相应池中的氧传 递系数为控制量;

　　S2.模糊神经网络模型：

　　采用TSK模型的形式，输出变量见式(1)所示：

　　$y(x_1,x_2,..,x_4)=\underset{j=1}{\overset{u}{\Sigma }}{w}_j\&CenterDot;{\phi }_j={\Theta }^T\left(k\right)\Psi \left(k\right)---\left(1\right)$

　　其中，u是训练所得到的模糊规则个数，wj是模糊系统的结论权值，φj为模 糊系统的各隶属度函数，令Aj=(α1j,α2j,...,αrj)，α表示wj的参数，X=(x1,x2,…,xr)， 则Ψ(k)=[φ1X,..,φuX]T;

　　S3.反馈线性化思想：

　　反馈线性化是一种非线性控制器设计方法，它的中心思想是把一个非线性 系统通过线性变换动态地(局部或者整体地)转换成近似等价的线性系统;

　　考虑如下的一类非线性离散系统动态模型：

　　$\left\{\begin{array}{c}{x}_n(k+1)=f\left[x\left(k\right)\right]+g\left[x\left(k\right)\right]u\left(k\right)\\ y(k+1)=x_n(k+1)\end{array}\right.---\left(2\right)$

　　其中，x(k)=[x1(k),x2(k),..,xn(k)]T=[x(k),x(k-1),..,x(k-n+1)]T是系统状态向量，u是 系统输入，y是系统输出，f[x(k)]和g[x(k)]是未知函数;

　　假定|g[x(k)]>ε成立，其中ε是一个足够小的正实数，由此可以得知模糊模型 的相对度等于1;

　　针对上述所示的非线性系统(假设Lh[x(k)]g[x(k)]=g[x(k)]≠0)，选择如下的控制 率：

　　$u_{*}=\frac{1}{g\left[x\left(k\right)\right]}[-f[x\left(k\right)]+v\left(k\right)]---\left(3\right)$

　　而对于控制目标是跟踪指定轨迹xnd的情况，且该预定轨迹是有界的，可以 选择v(k)：

　　v(k)=xnd(k+1)-kne(k-n+1)-…-k1e(k)=xnd(k+1)-kTe(k) (4)

　　其中，e(k)=x(k)-xd(k)是跟踪误差，e(k)=[e(k-n+1),...,e(k-1),e(k)]T， k=[kn,kn-1,..,k1]T，以使得系统输出可以渐进收敛到指定轨迹，此时可以得到系统 闭环误差方程为：

　　e(k+1)=-kTe(k) (5)

　　然而，由于污水系统运行机理的复杂性，系统状态方程式中的f[x(k)]和g[x(k)] 在这里都是未知函数，使得上述中的控制输入式(3)的表达式在污水处理系统 溶解氧控制器设计中是不可用的，因此不能得到上述误差闭环方程;

　　由此，将式(4)带入式(3)中，并与式(2)相减得到下式(6)，得到系 统输出误差与控制率之间的闭环动态方程：

　　e(k+1)=-kTe(k)+g[u*(k)-u(k)] (6)

　　S4.设计广义预测控制器

　　广义预测控制算法中，采用公式(7)所示的受控自回归积分滑动平均模型 (CARIMA)作为被控系统的数学模型;

　　A(z-1)y(t)=B(z-1)u(t-1)+C(z-1)w(t)/Δ (7)

　　其中，A(z-1)、B(z-1)和C(z-1)是z-1的多项式，z-1表示后移算子，w(t)是系统 干扰;

　　利用Diophantine方程的方法求得广义预测控制律为：

　　u=(GTG+λI)-1GT[yr-Fy(t)-HΔu(t-1)] (8)

　　其中，F、G、H表示所采用Diophantine方程求解控制律的参数向量，λ表 示控制权值，yr表示指定参考轨迹，y(t)表示系统输出，Δu(t-1)表示所求的控制 增量，I表示单位向量;

　　S5.设计T-S模糊模型结论参数的自适应规则

　　由系统输出误差与控制率之间的闭环动态方程的向量形式见式(9)：

　　e(k+1)=Λe(k)+bg[u*(k)-u(k)] (9)

　　其中Λ、bg是闭环动态方程的参数，u*(k)是所选择的期望控制率;

　　由广义预测控制算法得到的控制增量，得到如下的广义预测控制的控制率， 如式(10)所示：

　　u(k)=K[ΦR-Fy(k)]+u(k-1) (10)

　　K=GT/(GTG+λ)

　　其中，G、F是求解广义预测控制率过程中所用到的参数，R是指定轨迹， λ是控制加权常数，u(k)表示控制变量，y(k)表示被控变量，Φ表示反馈增益向量， 这里取作单位向量;

　　由动态模糊神经网络建模方法得到的系统模型式(1)作为上述控制率 表达式中的系统输出y(k)的估计，从而可以得到该控制率u(k)以及相应的最优控 制率u*(k)为：

　　$\begin{array}{c}u\left(k\right)=u[x_e\left(k\right),\hat{\Theta }]\\ =K[\mathrm{\Phi R}-F\hat{y}\left(k\right)]+u(k+1)\\ =K[\mathrm{\Phi R}-F{\hat{\Theta }}^T\left(k\right)\Psi \left(k\right)]+u(k+1)\end{array}---\left(11\right)$

　　u*(k)=u[xe(k),Θ*] (12)

　　其中，Ψ(k)为模糊神经网络模型系数组合成的参数，Θ*为最优参数向量; 并以u*作为控制率的最优近似，代入到式(9)中，得到系统误差与广义预测控 制率相关联的系统误差表达式(13)：

　　$\begin{array}{c}e(k+1)=\mathrm{\Lambda e}\left(k\right)+b_g[u^{*}\left(k\right)-u\left(k\right)]\\ =\mathrm{\Lambda e}\left(k\right)+b_g\mathrm{KF}{\hat{\Theta }}^T\left(k\right)\Psi \left(k\right)\end{array}---\left(13\right)$

　　其中，$\tilde{\Theta }\left(k\right)=\hat{\Theta }\left(k\right)-{\Theta }^{*};$

　　考虑如下的李雅普诺夫候选函数V(k)(即可以证明系统在某平衡点的稳定性 的函数)，其中r是一个正整数;

　　$V\left(k\right)=\frac{1}{2}{e}^T\left(k\right)\mathrm{Pe}\left(k\right)+\frac{1}{2\gamma }{\hat{\Theta }}^T(k+1)\hat{\Theta }(k-1)---\left(14\right)$

　　其中P是所设的一个正定对称矩阵，γ是一个正整数;

　　为了使跟踪误差收敛到0，根据李雅普诺夫稳定性定理，需要使得ΔV(k)<0， 最终得到模型参数的自适应变化率规则如式(15)所示：

　　$\hat{\Theta }\left(k\right)=\hat{\Theta }(k-1)+\gamma {\left[\mathrm{\Lambda e}\left(k\right)\right]}^{T}P{b}_g\mathrm{KF\Psi }\left(k\right)---\left(15\right)$

　　这个TSK模糊模型结论参数的自适应变化率的意义在于，它会影响到广义 预测控制增量，并根据式(13)那样，使得系统跟踪误差收敛;到这里，系统 跟踪误差收敛下的模型参数自适应证明完毕;

　　S6.应用到BSM1中的溶解氧浓度控制

　　基于TSK模糊模型设计的广义预测控制器，在应用到BSM1中运行过程中， 由式(15)根据系统运行状态动态调整模糊模型结论参数，使其反映系统此时 的动态特性，进而影响到广义预测控制律;通过对A2/O活性污泥处理系统的好 氧池的氧传递系数进行调节，实现溶解氧浓度的稳态控制。

　　本发明的另一目的通过以下的技术方案来实现：

　　一种污水处理过程自适应广义预测控制系统，包括顺序相连的GPC控制器、 污水控制模块、反馈线性化模块、广义预测控制器，其中GPC控制器与广义预 测控制器相连。

　　所述的广义预测控制器是基于TSK模糊模型设计的。

　　本发明与现有技术相比，具有如下优点和有益效果：

　　1、它利用了广义动态模糊神经网络可以较好模拟系统复杂关系的特性，同 时利用了广义预测控制的鲁棒性等特性。该控制算法可以在污水处理过程中根 据入水状态、系统输出误差来自适应的调整所采用模糊模型的结论参数，以实 时反映此时系统的特性，最终使得溶解氧浓度稳定在设定值附近，达到控制目 的。

　　2、该控制算法解决了普通广义预测控制在应对较大干扰时不能实现稳定控 制的问题。实验结果表明该控制算法能够稳定、快速地控制溶解氧浓度，具有 较强的抗干扰能力，有利于实现污水处理过程的稳定、高效运行。