基于神经网络的污水处理过程出水总磷TP软测量方法

发布时间：2018-5-20 17:52:16  中国污水处理工程网

　　申请日2014.09.05

　　公开(公告)日2014.12.03

　　IPC分类号G06N3/02; G01N33/18; G06N3/08

　　摘要

　　本发明提出一种基于神经网络的污水处理过程出水总磷TP软测量方法，属于污水处理领域。污水处理过程机理复杂，为使污水处理系统处于良好的运行工况，获得更好的出水水质，需要对污水处理系统中的过程参数及水质参数进行检测。针对当前污水处理厂出水总磷无法实时获取的问题，本发明提出一种基于自组织径向基神经网络建立的软测量模型。根据自组织方法确定神经网络的初始结构和初始参数，简化神经网络结构，对出水总磷TP进行实时软测量。根据软测量结果，对污水处理过程中的相关控制环节及生化反应中的物料调节，提高污水处理的出水水质质量，为污水处理过程安全、平稳运行提供理论支撑与技术保障。

　　权利要求书

　　1.一种基于神经网络的污水处理过程出水总磷TP软测量方法，其特征在 于，包括如下步骤：

　　步骤1：特征变量的选取

　　软测量模型特征变量的选取分为主要变量的选取和辅助变量的选取，以出水 总磷TP浓度为主要变量，通过主元分析法，确定污泥回流量、泥龄、酸碱度PH、 氧化还原电位ORP、进水氨氮NH3-N、进水氯CL、出水5日生物需氧量BOD5、 出水悬浮物浓度SS和前一时刻的出水总磷TP为辅助变量;

　　步骤2：设计用于预测出水总磷TP的特征模型

　　对从污水处理厂获得的变量数据进行归一化处理，方法如下：

　　$D*\frac{D-D_{\min }}{D_{\max }-D_{\min }}$

　　其中D*表示归一化后的数据，Dmin为原序列数据中的最小值，Dmax为原序 列数据中的最大值，经过归一化处理后，所有的变量数据都被归一化到[0,1]之间; 用于出水总磷的自组织RBF网络拓扑结构分为三层：输入层、隐含层、输出层; 输入为污泥回流量、泥龄、酸碱度PH、氧化还原电位ORP、进水氨氮NH3-N、 进水氯CL、出水5日生物需氧量BOD5、出水悬浮物浓度SS和前一时刻的出水 总磷TP，输出为出水总磷TP;

　　步骤2.1：初始化神经网络

　　初始时刻，神经网络的结构为9-0-1的连接方式，输入层有9个节点，隐含 层没有节点，输出层有1个节点，神经网络的输入向量表示为x=(x1,x2,...,x9)T; 输出层输出的是出水总磷TP的值，输出层的节点数为1;在t时刻，神经网络 的输出向量表示为y(ι)，计算方法如下：

　　$y\left(i\right)=\underset{j=1}{\overset{J}{\Sigma }}{w}_{\mathrm{ji}}{\Phi }_j$

　　其中y(i)为第i个输入向量xi进入网络时的对应输出，wji为j个隐节点到输 出节点的连接权值，Φj为j个隐节点的传递函数，隐含层神经元的传递函数为高 斯函数，如下所示：

　　${\Phi }_j\left(x_i\right)=e^{-\frac{{\left|\right|x_i-c_j\left|\right|}^2}{2{\delta }_j^2}}$

　　其中，Φj(xi)表示第i个输入向量xi进入网络时第j个隐节点的对应输出，cj为第j个隐节点的中心向量，δj为第j个隐节点的宽度值;

　　步骤2.2：性能指标函数

　　$E=\frac{1}{2}\underset{i=1}{\overset{N}{\Sigma }}{(y_{\mathrm{di}}-y_i)}^2$

　　其中，ydi为第i个样本对应的期望输出,yi为第i个样本对应的网络输出， N为参与训练的样本的个数;

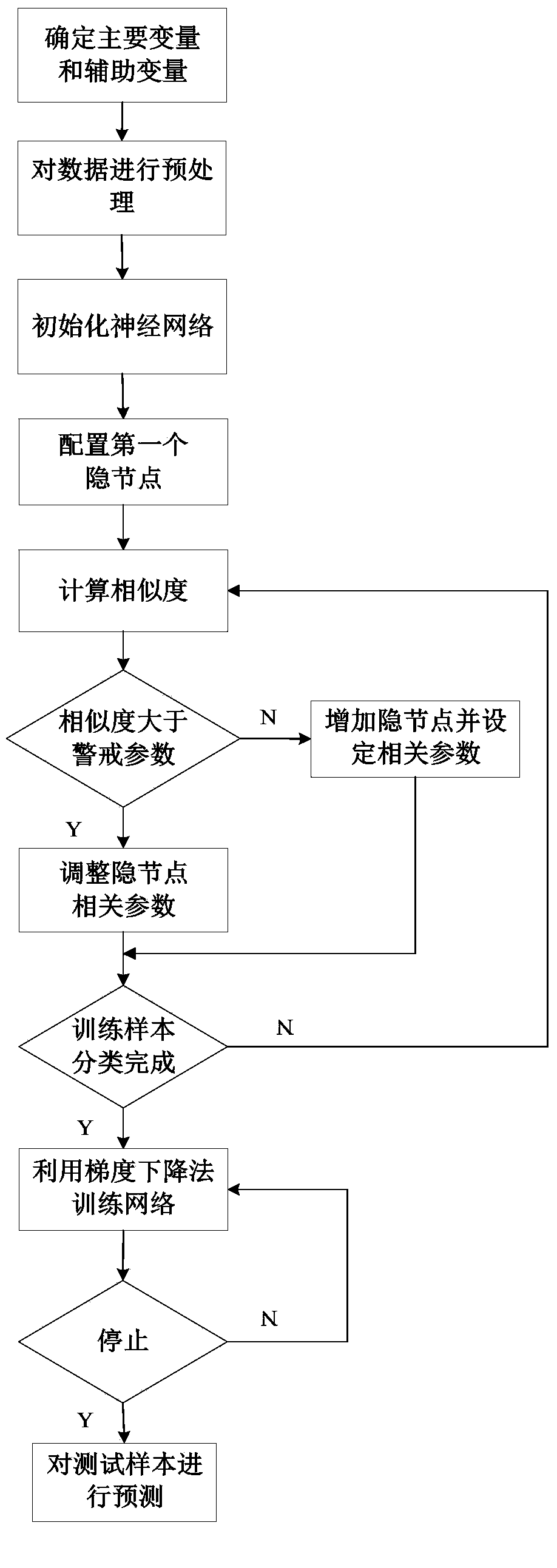
　　步骤3：神经网络结构自组织设计

　　步骤3.1：当第1个数据进入网络后，为网络分配1个隐含层节点，同时， 将第1个数据的输入向量赋予第1个隐节点，作为其中心向量;将第1个样本的 期望输出向量作为第1个隐节点到输出节点的连接权值;则第1个隐节点的中心 向量和第一个隐节点到输出节点的连接权值表示如下：

　　c1=x1=(x11,x12,...,x19)T

　　w1=yd1

　　其中，x1为第一个样本的输入向量，yd1为第一个样本的期望输出值;

　　步骤3.2：在k时刻，假设已经存在j个隐节点，当第k个数据样本进入网 络时，则需要对第k个输入向量与已存的j个隐节点的中心向量的相似度进行比 较，方法如下：

　　$s(x_k,c_j)=1-\frac{\mathrm{dist}(x_k,c_j)}{\left|\right|x_k\left|\right|+\left|\right|c_j\left|\right|}$

　　其中，xk为第k个样本的输入向量，cj为第j个隐节点的中心向量，找出与 第k个输入向量相似度最高的隐节点l，将最大的相似度值与警戒参数V进行比 较;

　　当s(xk,cl)≥V时，认为第l个隐节点与第k个输入向量的相似度足够大，当 前网络能够对新数据进行学习，对第l个隐节点的参数进行调整，方法如下：

　　nl=nl+1

　　$c_l=\frac{n_l{c}_l+x_k}{n_l+1}$

　　$w_l=\frac{n_l{w}_l+y_{\mathrm{dk}}}{n_l+1}$

　　其中，nl为第l个隐节点的样本数量所覆盖的样本数量，cl为第l个隐节点 的中心向量，wl为l个隐节点到输出节点的连接权值，ydk为第k个样本对应的 期望输出;

　　当s(xk,cl)

　　cj+1=xk

　　wj+1=ydk

　　其中，cj+1为新增隐节点的中心向量，wj+1为新增隐节点到输出节点的连接 权值，xk为第k个样本的输入向量，ydk为第k个样本对应的期望输出;

　　步骤3.3：宽度参数设置

　　在对隐节点中心向量和连接权值进行设置的同时，需要对隐节点宽度进行设 置，由高斯函数的特性得到如下关系：

　　$\left\{\begin{array}{c}\left|\right|x-c\left|\right|\le \sigma ,f\left(x\right)\≥0.3679\\ \left|\right|x-c\left|\right|\le 2\sigma ,f\left(x\right)\≥0.0183\end{array}\right.$

　　径向基神经元的输出越大代表该神经元在网络中的显著性越大，因此本发明 设置如下：

　　当||x-c||≤λσ时，

　　Φ(x)≥0;

　　即当输入向量、中心向量与宽度值满足如上所示的关系时，神经元才能被激 活，其中λ为比例因子;

　　由相似度比较公式得：

　　dist(xk,cl)≤(1-V)(||xk||+||cl||)

　　联立可得：

　　σl=(1-V)(||xk||+||cl||)/λ

　　步骤4：神经网络训练

　　步骤4.1：对神经网络进行训练，选取均方误差函数作为性能指标，方法如 下：

　　$E=\frac{1}{2}\underset{i=1}{\overset{N}{\Sigma }}{(y_{\mathrm{di}}-y_i)}^2$

　　其中，ydi为第i个样本对应的期望输出,yi为第i个样本对应的网络输出， N为参与训练的样本的个数;

　　步骤4.2：采用梯度训练法对神经网络进行训练，对第j个隐节点高斯函数 中心向量训练，方法如下：

　　$c_j(k+1)=c_j\left(k\right)-{\eta }_c\frac{\∂E\left(k\right)}{\∂c_j\left(k\right)}$

　　$\frac{\∂E\left(k\right)}{{\∂c}_j\left(k\right)}=-\frac{1}{{\sigma }_j^2}\underset{p=1}{\overset{N}{\Sigma }}(y_{\mathrm{dp}}-y_p)\·w_j\left(k\right)\times \phi \left(x_p\right)[x_p-c_j\left(k\right)]$

　　其中，k为训练过程中迭代到第k步，ηc是中心向量的学习率，N为参与 训练的样本的个数;

　　步骤4.3：对第j个隐节点高斯函数宽度值训练，方法如下：

　　${\sigma }_j(k+1)={\sigma }_j\left(k\right)-{\eta }_{\sigma }\frac{\∂E\left(k\right)}{\∂{\sigma }_j\left(k\right)}$

　　$\frac{\∂E\left(k\right)}{{\∂c}_j\left(k\right)}=-\frac{1}{{\sigma }_j^3}\underset{p=1}{\overset{N}{\Sigma }}(y_{\mathrm{dp}}-y_p)\·w_j\left(k\right)\times \phi \left(x_p\right){\left|\right|x_p-c_j\left(k\right)\left|\right|}^2$

　　其中，k为训练过程中迭代到第k步，ησ是宽度值的学习率，N为参与训 练的样本的个数;

　　步骤4.4：对第j个隐节点到输出节点连接权值训练，方法如下：

　　$w_j(k+1)=w_j\left(k\right)-{\eta }_w\frac{\∂E\left(k\right)}{\∂w_j\left(k\right)}$

　　$\frac{\∂E\left(k\right)}{{\∂w}_{\mathrm{jn}}\left(k\right)}=-\underset{p=1}{\overset{N}{\Sigma }}(y_{\mathrm{dp}}-y_p){\phi }_j\left(x_p\right)$

　　其中，k为训练过程中迭代到第k步，ηw是连接权值的学习率，N为参与 训练的样本的个数;

　　步骤5：用训练好的样本对测试样本进行预测

　　将测试样本数据作为训练好的神经网络的输入，神经网络的输出即为出水总 磷的预测结果。

　　说明书

　　一种基于神经网络的污水处理过程出水总磷TP软测量方法

　　技术领域

　　本发明基于自组织RBF神经网络建立城市污水处理过程出水总磷TP的软测 量模型。软测量是检测技术及仪表研究的主要发展趋势之一，是先进制造技术领 域的重要分支。本发明既属于污水处理领域，也属于检测技术及仪表研究技术领 域。

　　背景技术

　　《中华人民共和国国民经济和社会发展第十二个五年规划纲要》指出，要加 快建设全国城镇污水处理及再生利用设施、促进主要污染物减排、改善水环境质 量，到2015年，实现城市污水处理率达到85%的总体目标。为了达到这一目标， 从技术要层面来看，对于重点流域、重要水源地等敏感水域地区的城镇污水处理 设施，应根据水质目标和排污总量控制要求，选择具备除磷脱氮能力的工艺技术。 随着水体富营养化问题的日渐突出，污水综合排放标准日趋严格，使得污水处理 技术逐渐从以单一去除有机物为目的的阶段进入既要除有机物又要脱氮除磷的 深度处理阶段。因此，对污水处理过程水质参数总磷TP的测量是至关重要的。

　　污水处理过程是一个复杂的生化反应过程，由于测量技术的局限，污水处理 过程中的一些重要参数是难以精确测量的。目前污水总磷TP的测量方法主要为 化学测量法和仪表检测法，前者耗时较长，滞后于污水处理过程，不能及时检测 出水水质，同时由于化学实验的随机性，也难以保证检测的准确性;另一方面检 测仪表价格昂贵且使用维护困难，检测仪表的精密性也会给出水总磷TP的实时 检测造成一定的影响，这都说明了当前出水总磷TP检测的局限性。因此对出水 总磷TP实时检测问题的研究是具有重要现实意义。

　　近年来，软测量技术被广泛应用于污水处理过程水质参数的特征建模中，其 中以神经网络作为软测量工具的方法研究最为活跃。本发明提出了一种基于自组 织RBF神经网络的软测量方法，通过构建总磷与其它易测辅助变量之间的关系， 实现对出水总磷TP的实时检测，提高出水总磷TP测量质量及污水处理过程的 监测能力，具有广泛的应用前景和重要的现实意义。

　　发明内容

　　针对现有方法存在的不足，本发明提出一种基于自组织径向基(RBF)神经网 络的总磷TP软测量方法，分析总结与总磷TP密切相关的易测辅助变量，确定 神经网络模型的输入量，基于自组织方法，设计网络结构，建立总磷TP的软测 量模型，实现对出水总磷TP的实时检测，解决污水出水总磷TP难以测量的问 题。

　　一种基于神经网络的污水处理过程出水总磷TP软测量方法，其特征在于， 包括如下步骤：

　　步骤1：特征变量的选取

　　软测量模型特征变量的选取分为主要变量的选取和辅助变量的选取，以出水 总磷TP浓度为主要变量，通过主元分析法，确定污泥回流量、泥龄、酸碱度PH、 氧化还原电位ORP、进水氨氮NH3-N、进水氯CL、出水5日生物需氧量BOD5、 出水悬浮物浓度SS和前一时刻的出水总磷TP为辅助变量;

　　步骤2：设计用于预测出水总磷TP的特征模型

　　对从污水处理厂获得的变量数据进行归一化处理，方法如下：

　　$D*\frac{D-D_{\min }}{D_{\max }-D_{\min }}---\left(1\right)$

　　其中D*表示归一化后的数据，Dmin为原序列数据中的最小值，Dmax为原序 列数据中的最大值，经过归一化处理后，所有的变量数据都被归一化到[0,1]之间; 用于出水总磷的自组织RBF网络拓扑结构分为三层：输入层、隐含层、输出层; 输入为污泥回流量、泥龄、酸碱度PH、氧化还原电位ORP、进水氨氮NH3-N、 进水氯CL、出水5日生物需氧量BOD5、出水悬浮物浓度SS和前一时刻的出水 总磷TP，输出为出水总磷TP;

　　步骤2.1：初始化神经网络

　　初始时刻，神经网络的结构为9-0-1的连接方式，输入层有9个节点，隐含 层没有节点，输出层有1个节点，神经网络的输入向量表示为x=(x1,x2,...,x9)T; 输出层输出的是出水总磷TP的值，输出层的节点数为1;在t时刻，神经网络 的输出向量表示为y(ι)，计算方法如下：

　　$y\left(i\right)=\underset{j=1}{\overset{J}{\Sigma }}{w}_{\mathrm{ji}}{\Phi }_j---\left(2\right)$

　　其中y(i)为第i个输入向量xi进入网络时的对应输出，wji为j个隐节点到输 出节点的连接权值，Φj为j个隐节点的传递函数，隐含层神经元的传递函数为高 斯函数，如下所示：

　　${\Phi }_j\left(x_i\right)=e^{-\frac{{\left|\right|x_i-c_j\left|\right|}^2}{2{\delta }_j^2}}---\left(3\right)$

　　其中，Φj(xi)表示第i个输入向量xi进入网络时第j个隐节点的对应输出，cj为第j个隐节点的中心向量，δj为第j个隐节点的宽度值;

　　步骤2.2：性能指标函数

　　$E=\frac{1}{2}\underset{i=1}{\overset{N}{\Sigma }}{(y_{\mathrm{di}}-y_i)}^2---\left(4\right)$

　　其中，ydi第i个样本对应的期望输出,yi为第i个样本对应的网络输出，N 为参与训练的样本的个数;

　　步骤3：神经网络结构自组织设计

　　步骤3.1：当第1个数据进入网络后，为网络分配1个隐含层节点，同时， 将第1个数据的输入向量赋予第1个隐节点，作为其中心向量;将第1个样本的 期望输出向量作为第1个隐节点到输出节点的连接权值;则第1个隐节点的中心 向量和第一个隐节点到输出节点的连接权值表示如下：

　　c1=x1=(x11,x12,...,x19)T (5)

　　w1=yd1 (6)

　　其中，x1为第一个样本的输入向量，yd1为第一个样本的期望输出值;

　　步骤3.2：在k时刻，假设已经存在j个隐节点，当第k个数据样本进入网 络时，则需要对第k个输入向量与已存的j个隐节点的中心向量的相似度进行比 较，方法如下：

　　$s(x_k,c_j)=1-\frac{\mathrm{dist}(x_k,c_j)}{\left|\right|x_k\left|\right|+\left|\right|c_j\left|\right|}---\left(7\right)$

　　其中，xk为第k个样本的输入向量，cj为第j个隐节点的中心向量，找出与 第k个输入向量相似度最高的隐节点l，将最大的相似度值与警戒参数V进行比 较;

　　当s(xk,cl)≥V时，认为第l个隐节点与第k个输入向量的相似度足够大，当 前网络能够对新数据进行学习，对第l个隐节点的参数进行调整，方法如下：

　　nl=nl+1 (8)

　　$c_l=\frac{n_l{c}_l+x_k}{n_l+1}---\left(9\right)$

　　$w_l=\frac{n_l{w}_l+y_{\mathrm{dk}}}{n_l+1}---\left(10\right)$

　　其中，nl为第l个隐节点的样本数量所覆盖的样本数量，cl为第l个隐节点 的中心向量，wl为l个隐节点到输出节点的连接权值，ydk为第k个样本对应的 期望输出;

　　当s(xk,cl)

　　cj+1=xk (11)

　　wj+1=ydk (12)

　　其中，cj+1为新增隐节点的中心向量，wj+1为新增隐节点到输出节点的连接 权值，xk为第k个样本的输入向量，ydk为第k个样本对应的期望输出;

　　步骤3.3：宽度参数设置

　　在对隐节点中心向量和连接权值进行设置的同时，需要对隐节点宽度进行设 置，由高斯函数的特性得到如下关系：

　　$\left\{\begin{array}{c}\left|\right|x-c\left|\right|\le \sigma ,f\left(x\right)\≥0.3679\\ \left|\right|x-c\left|\right|\le 2\sigma ,f\left(x\right)\≥0.0183\end{array}\right.---\left(13\right)$

　　径向基神经元的输出越大代表该神经元在网络中的显著性越大，因此本发明 设置如下：

　　当||x-c||≤λσ时， (14)

　　Φ(x)≥0; (15)

　　即当输入向量、中心向量与宽度值满足如上所示的关系时，神经元才能被激 活，其中λ为比例因子;

　　由相似度比较公式得：

　　dist(xk,cl)≤(1-V)(||xk||+||cl||) (16)

　　联立可得：

　　σl=(1-V)(||xk||+||cl||)/λ (17)

　　步骤4：神经网络训练

　　步骤4.1：对神经网络进行训练，选取均方误差函数作为性能指标，方法如 下：

　　$E=\frac{1}{2}\underset{i=1}{\overset{N}{\Sigma }}{(y_{\mathrm{di}}-y_i)}^2---\left(18\right)$

　　其中，ydi为第i个样本对应的期望输出，yi为第i个样本对应的网络输出， N为参与训练的样本的个数;

　　步骤4.2：采用梯度训练法对神经网络进行训练，对第j个隐节点高斯函数 中心向量训练，方法如下：

　　$c_j(k+1)=c_j\left(k\right)-{\eta }_c\frac{\∂E\left(k\right)}{\∂c_j\left(k\right)}---\left(19\right)$

　　$\frac{\∂E\left(k\right)}{{\∂c}_j\left(k\right)}=-\frac{1}{{\sigma }_j^2}\underset{p=1}{\overset{N}{\Sigma }}(y_{\mathrm{dp}}-y_p)\·w_j\left(k\right)\times \phi \left(x_p\right)[x_p-c_j\left(k\right)]---\left(20\right)$

　　其中，k为训练过程中迭代到第k步，ηc是中心向量的学习率，N为参与 训练的样本的个数;

　　步骤4.3：对第j个隐节点高斯函数宽度值训练，方法如下：

　　${\sigma }_j(k+1)={\sigma }_j\left(k\right)-{\eta }_{\sigma }\frac{\∂E\left(k\right)}{\∂{\sigma }_j\left(k\right)}---\left(21\right)$

　　$\frac{\∂E\left(k\right)}{{\∂c}_j\left(k\right)}=-\frac{1}{{\sigma }_j^3}\underset{p=1}{\overset{N}{\Sigma }}(y_{\mathrm{dp}}-y_p)\·w_j\left(k\right)\times \phi \left(x_p\right){\left|\right|x_p-c_j\left(k\right)\left|\right|}^2---\left(22\right)$

　　其中，k为训练过程中迭代到第k步，ησ是宽度值的学习率，N为参与训 练的样本的个数;

　　步骤4.4：对第j个隐节点到输出节点连接权值训练，方法如下：

　　$w_j(k+1)=w_j\left(k\right)-{\eta }_w\frac{\∂E\left(k\right)}{\∂w_j\left(k\right)}---\left(23\right)$

　　$\frac{\∂E\left(k\right)}{{\∂w}_{\mathrm{jn}}\left(k\right)}=-\underset{p=1}{\overset{N}{\Sigma }}(y_{\mathrm{dp}}-y_p){\phi }_j\left(x_p\right)---\left(24\right)$

　　其中，k为训练过程中迭代到第k步，ηw是连接权值的学习率，N为参与 训练的样本的个数;

　　步骤5：用训练好的样本对测试样本进行预测

　　将测试样本数据作为训练好的神经网络的输入，神经网络的输出即为出水总 磷的预测结果。

　　本发明与现有技术相比，具有以下明显的优势和有益效果：

　　1、本发明根据径向基神经网络具有良好非线性映射能力的特点，针对当前 污水处理过程出水总磷测量存在的不足，采用自组织径向基神经网络实现辅助变 量与总磷TP之间的非线性映射，建立了污水处理过程出水总磷的软测量模型， 实现对出水总磷TP的软测量，具有实时性好、稳定性好、精度高等特点。

　　2、本发明基于输入向量与隐层中心向量之间的相似度比较，实现了对神经 网络隐层结构的自组织设计，同时根据径向基函数的特性分析了参数间的关系， 实现了对参数的自适应调整，解决了径向基神经网络结构难以确定的问题，同时 也保证了网络的泛化性能。